drawPath 绘制自定义图形
上一篇说过,drawPath(path) 这个方法是通过描述路径的方式来绘制图形的,它的 path 参数就是用来描述图形路径的对象。
Path 可以描述直线、二次曲线、三次曲线、圆、椭圆、弧形、矩形、圆角矩形。把这些图形结合起来,就可以描述出很多复杂的图形。下面我就说一下具体的怎么把这些图形描述出来。
Path 有两类方法,一类是直接描述路径的,另一类是辅助的设置或计算。
Path 方法第一类:直接描述路径。
这一类方法还可以细分为两组:添加子图形和画线(直线或曲线)
第一组: addXxx() ——添加子图形
添加圆
addCircle(float x, float y, float radius, Direction dir)
x, y, radius 这三个参数是圆的基本信息,最后一个参数 dir 是画圆的路径的方向。
路径方向有两种:顺时针(CW clockwise)和逆时针(CWW counter-clockwise)。对于普通情况,这个参数是CW或者CWW,没有什么影响。它只是在需要填充图形,并且图形出现自相交时,用于判断填充范围的。
具体怎么做,下面 Path.setFillType() 的时候会详细介绍,而在这里可以先忽略 dir 这个参数。
1 | path.addCircle(250, 250, 200, Path.Direction.CW); |

可以看出,path.AddCircle(x, y, radius, dir) + canvas.drawPath(path, paint) 这种写法,和直接使用 canvas.drawCircle(x, y, radius, paint) 的效果是一样的,区别只是它的写法更复杂。所以如果只画一个圆,没必要用 Path,直接用 drawCircle() 就行了。drawPath() 一般是在绘制组合图形时才会用到的。
其他的 Path.add-() 方法和这类似,例如:
添加椭圆
addOval(float left, float top, float right, float bottom, Direction dir)
addOval(RectF oval, Direction dir)
添加矩形
addRect(float left, float top, float right, float bottom, Direction dir)
addRect(RectF rect, Direction dir)
添加圆角矩形
addRoundRect(RectF rect, float rx, float ry, Direction dir)
addRoundRect(float left, float top, float right, float bottom, float rx, float ry, Direction dir)
addRoundRect(RectF rect, float[] radii, Direction dir)
addRoundRect(float left, float top, float right, float bottom, float[] radii, Direction dir)
添加弧形
addArc(float left, float top, float right, float bottom, float startAngle, float sweepAngle)
addArc(RectF oval, float startAngle, float sweepAngle)
添加另一个 Path
addPath(Path path)
上面这几个方法和 addCircle() 的使用都差不多,不再做过多介绍。
第二组: xxxTo() ——画线(直线或曲线)
这一组和第一组 addXxx() 方法的区别在于,第一组是添加的完整封闭图形(除了 addPath() ),而这一组添加的只是一条线。
画直线
lineTo(float x, float y)
rLineTo(float x, float y)
从当前位置向目标位置画一条直线, x 和 y 是目标位置的坐标。这两个方法的区别是,lineTo(x, y) 的参数是绝对坐标,而 rLineTo(x, y) 的参数是相对当前位置的相对坐标 (前缀 r 指的就是 relatively 「相对地」)。
当前位置:所谓当前位置,即最后一次调用画 Path 的方法的终点位置。初始值为原点 (0, 0)。
1 | paint.setStyle(Style.STROKE); |
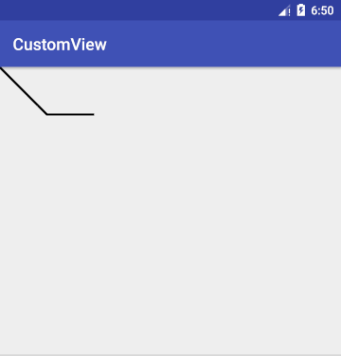
画二次贝塞尔曲线
quadTo(float x1, float y1, float x2, float y2)
rQuadTo(float dx1, float dy1, float dx2, float dy2)
这条二次贝塞尔曲线的起点就是当前位置,而参数中的 x1, y1 和 x2, y2 则分别是控制点和终点的坐标。和 rLineTo(x, y) 同理,rQuadTo(dx1, dy1, dx2, dy2) 的参数也是相对坐标。
画三次贝塞尔曲线
cubicTo(float x1, float y1, float x2, float y2, float x3, float y3)
rCubicTo(float x1, float y1, float x2, float y2, float x3, float y3)
cubicTo() 和 rCubicTo() 是三次贝塞尔曲线
贝塞尔曲线:贝塞尔曲线是几何上的一种曲线。它通过起点、控制点和终点来描述一条曲线,主要用于计算机图形学。概念总是说着容易听着难,总之使用它可以绘制很多圆润又好看的图形,但要把它熟练掌握、灵活使用却是不容易的。不过还好的是,一般情况下,贝塞尔曲线并没有什么用处,只在少数场景下绘制一些特殊图形的时候才会用到,所以如果你还没掌握自定义绘制,可以先把贝塞尔曲线放一放,稍后再学也完全没问题。
移动到目标位置
moveTo(float x, float y)
rMoveTo(float x, float y)
不论是直线还是贝塞尔曲线,都是以当前位置作为起点,而不能指定起点。通过 moveTo(x, y) 或 rMoveTo() 来改变当前位置,从而间接地设置这些方法的起点。
1 | path.lineTo(200, 200); |
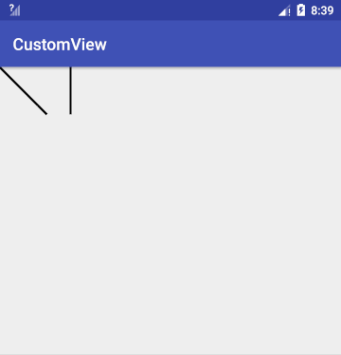
moveTo(x, y) 虽然不添加图形,但它会设置图形的起点,所以它是非常重要的一个辅助方
画弧形
arcTo(RectF oval, float startAngle, float sweepAngle, boolean forceMoveTo)
arcTo(float left, float top, float right, float bottom, float startAngle, float sweepAngle, boolean forceMoveTo)
arcTo(RectF oval, float startAngle, float sweepAngle)
这个方法和 Canvas.drawArc() 比起来,少了一个参数 useCenter,而多了一个参数 forceMoveTo 。
少了 useCenter ,是因为 arcTo() 只用来画弧形而不画扇形,所以不再需要 useCenter 参数;而多出来的这个 forceMoveTo 参数的意思是,绘制是要「抬一下笔移动过去」,还是「直接拖着笔过去」,区别在于是否留下移动的痕迹。
注意:不使用当前位置作为弧线的起点。
1 | //forceMoveTo 为true,抬一下笔移动过去 |
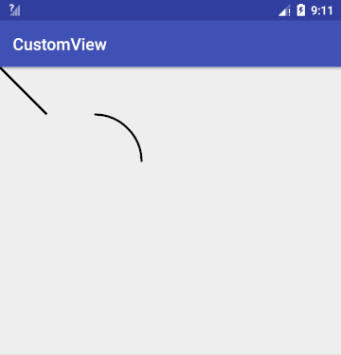
1 | //forceMoveTo 为true,直接拖着笔过去 |
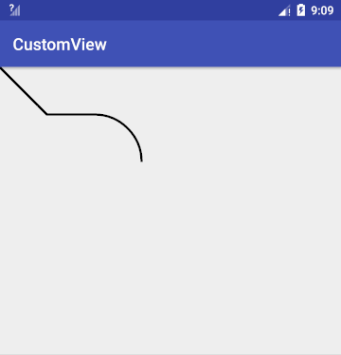
在第一组中有一个addArc()方法,也都是绘制弧形,只是addArc()默认直接使用了 forceMoveTo = true 的简化版 arcTo() 。
封闭当前子图形
close()
它的作用是把当前的子图形封闭,即由当前位置向当前子图形的起点绘制一条直线。
1 | path.moveTo(100, 100); |
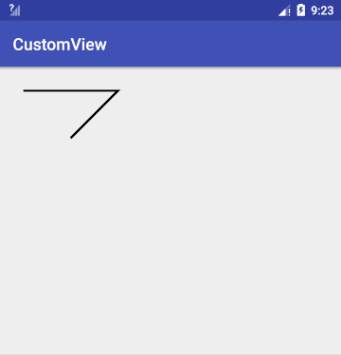
1 | path.moveTo(100, 100); |
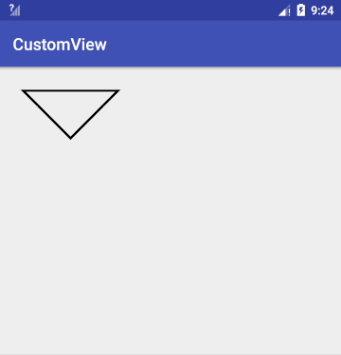
不是所有的子图形都需要使用 close() 来封闭。当需要填充图形时(即 Paint.Style 为 FILL 或 FILL_AND_STROKE),Path 会自动封闭子图形。
Path 方法第二类:辅助的设置或计算
这类方法的使用场景比较少,主要讲其中一个方法:setFillType(FillType fillType)。
Path.setFillType(Path.FillType ft) 设置填充方式
前面在说 dir 参数的时候提到, Path.setFillType(fillType) 是用来设置图形自相交时的填充算法的:

方法中填入不同的 FillType 值,就会有不同的填充效果。FillType 的取值有四个:
EVEN_ODDWINDING(默认值)INVERSE_EVEN_ODDINVERSE_WINDING
其中后面的两个带有 INVERSE_ 前缀的,只是前两个的反色版本,所以只要把前两个,即 EVEN_ODD 和 WINDING,搞明白就可以了。
EVEN_ODD 和 WINDING 的原理有点复杂,直接讲出来的话信息量太大,所以我先给一个简单粗暴版的总结,你感受一下: WINDING 是「全填充」,而 EVEN_ODD 是「交叉填充」:

之所以叫「简单粗暴版」,是因为这些只是通常情形下的效果;而如果要准确了解它们在所有情况下的效果,就得先知道它们的原理,即它们的具体算法。
EVEN_ODD 和 WINDING 的原理
EVEN_ODD
即 even-odd rule (奇偶原则):对于平面中的任意一点,向任意方向射出一条射线,这条射线和图形相交的次数(相交才算,相切不算哦)如果是奇数,则这个点被认为在图形内部,是要被涂色的区域;如果是偶数,则这个点被认为在图形外部,是不被涂色的区域。还以左右相交的双圆为例:

射线的方向无所谓,同一个点射向任何方向的射线,结果都是一样的,不信你可以试试。
从上图可以看出,射线每穿过图形中的一条线,内外状态就发生一次切换,这就是为什么 EVEN_ODD 是一个「交叉填充」的模式。
WINDING
即 non-zero winding rule (非零环绕数原则):首先,它需要你图形中的所有线条都是有绘制方向的:

然后,同样是从平面中的点向任意方向射出一条射线,但计算规则不一样:以 0 为初始值,对于射线和图形的所有交点,遇到每个顺时针的交点(图形从射线的左边向右穿过)把结果加 1,遇到每个逆时针的交点(图形从射线的右边向左穿过)把结果减 1,最终把所有的交点都算上,得到的结果如果不是 0,则认为这个点在图形内部,是要被涂色的区域;如果是 0,则认为这个点在图形外部,是不被涂色的区域。

和
EVEN_ODD相同,射线的方向并不影响结果。
所以,我前面的那个「简单粗暴」的总结,对于 WINDING 来说并不完全正确:如果你所有的图形都用相同的方向来绘制,那么 WINDING 确实是一个「全填充」的规则;但如果使用不同的方向来绘制图形,结果就不一样了。
图形的方向:对于添加子图形类方法(如
Path.addCircle()Path.addRect())的方向,由方法的dir参数来控制,这个在前面已经讲过了;而对于画线类的方法(如Path.lineTo()Path.arcTo())就更简单了,线的方向就是图形的方向。
所以,完整版的 EVEN_ODD 和 WINDING 的效果应该是这样的:

而 INVERSE_EVEN_ODD 和 INVERSE_WINDING ,只是把这两种效果进行反转而已,懂了 EVEN_ODD 和 WINDING,自然也就懂 INVERSE_EVEN_ODD 和 INVERSE_WINDING 了。
关于drawPath()差不多这么多,图形简单时,使用 drawCircle() drawRect() 等方法来直接绘制;图形复杂时,使用 drawPath() 来绘制自定义图形。
